/ G ψ = E ψ = IGFF   E [tG+].... ..  

Dispersão de Rutherford NA MECÂNICA GENERALZIADA GRACELI.

Em física, a dispersão de Rutherford é um fenômeno que foi explicado por Ernest Rutherford em 1909,^[1] e levou ao desenvolvimento da teoria orbital do átomo. É agora explorado pela técnica de análise de materiais espectrometria de dispersão de Rutherford. A dispersão de Rutherford é também referida às vezes como dispersão de Coulomb porque baseia-se em forças eletrostáticas (Coulomb). Um processo similar provou o interior do núcleo nos anos 1960, chamado dispersão profunda inelástica.

Destaques da experiência de Rutherford

• Um feixe de partículas alfa é direcionado a uma folha de ouro fina.
• Muitas das partículas passaram através da película sem sofrer desvio.
• Outras foram desviadas por diversos ângulos.
• Algumas inverteram o sentido do movimento.

A partir destes resultados, Rutherford concluiu que a maioria da massa era concentrada numa região minúscula, positivamente carregada (o núcleo), rodeada por electrões. Quando uma partícula alfa (positiva) se aproximava o suficiente do núcleo, era fortemente repelida.^[2] O pequeno tamanho do núcleo explicou a pequena quantidade de partículas alfa que foram repelidas em ângulos maiores. Rutherford demonstrou usando o método abaixo, que o tamanho do núcleo era inferior do que cerca de ${\displaystyle \scriptstyle 10^{-14}}$

Teoria de Dispersão

Geometria de dispersão de Rutherford.

Principais pressupostos:

• Colisão entre uma carga pontual, mais um núcleo pesado com carga Q=Ze é um projétil leve com carga q=ze é considerada como sendo elástica.

• Momento e energia são conservados.

• As partículas interagem através da força de Coulomb.

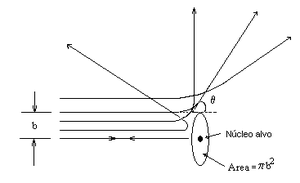
• A distância vertical onde o projétil se encontra a partir do centro do alvo, o parâmetro de impacto b , determinam o ângulo de dispersão θ.

A relação entre o ângulo de dispersão θ, a energia cinética inicial

${\displaystyle E=z{\frac {1}{2}}m.v_{o}^{2}}$ / G ψ = E ψ = IGFF   E [tG+].... ..  

e o parâmetro de impacto b é dado pela relação

${\displaystyle b={\frac {zZ}{2K}}.{\frac {e^{2}}{4\pi \varepsilon _{o}}}{\text{cot}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}$ (1,1) / G ψ = E ψ = IGFF   E [tG+].... ..  

onde z = 2, para partículas-α e Z = 79 de ouro.

Dedução da Transversal Diferencial

Na Figura , uma partícula que atinge o anel entre b e b + db é desviada num ângulo sólido dΩ entre θ e θ + dθ.

Por definição, a secção transversal é a constante de proporcionalidade

${\displaystyle 2\pi b.db=-\sigma (\theta ).2\pi .\operatorname {sen} \theta .d\theta }$ / G ψ = E ψ = IGFF   E [tG+].... ..  

então

${\displaystyle d\sigma =2\pi b|db|={\Bigg (}{\frac {d\sigma }{d\Omega }}{\Bigg )}.d\Omega }$ (1,2) / G ψ = E ψ = IGFF   E [tG+].... ..  

onde ${\displaystyle d\Omega =2\pi .\operatorname {sen} \theta .d\theta }$ / G ψ = E ψ = IGFF   E [tG+].... ..  

A seção transversal diferencial torna-se então

${\displaystyle {\frac {d\sigma }{d\Omega }}={\frac {2\pi b|db|}{2\pi .\operatorname {sen} \theta .d\theta }}}$ (1,3) / G ψ = E ψ = IGFF   E [tG+].... ..  

A partir da Equações 1,1 e 1,3 nós temos

${\displaystyle {\frac {d\sigma }{d\Omega }}={\Bigg (}{\frac {1}{4\pi \varepsilon _{o}}}{\Bigg )}^{2}{\Bigg (}{\frac {qQ}{4K_{\alpha }}}{\Bigg )}^{2}.{\frac {1}{\operatorname {sen} ^{4}}}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}$ (1.4) / G ψ = E ψ = IGFF   E [tG+].... ..  

A Eq.1.4, é chamada seção transversal diferencial para a dispersão de Rutherford.

Nos cálculos acima, considera-se apenas uma única partícula alfa. Num experimento de dispersão, é preciso considerar vários eventos de dispersão e medir-se a fracção de partículas desviadas num determinado ângulo.

Para um detector em um ângulo específico em relação ao feixe incidente, o número de partículas por unidade de superfície, colidindo o detector, é dado pela fórmula de Rutherford:

${\displaystyle N(\theta )={\frac {N_{i}.nLZ^{2}k^{2}.e^{4}}{4.r^{2}k.E^{2}\operatorname {sen} ^{4}{\Bigg (}{\frac {\theta }{2}}{\Bigg )}}}}$ / G ψ = E ψ = IGFF   E [tG+].... ..  

Verificação da fórmula de Rutherford

Onde:

Ni = número de partículas alfa incidentes;

n = átomos por unidade de volume no alvo;

L = espessura do alvo;

Z = número atómico do alvo;

e = carga electrónica;

k = constante de Coulomb;

r = distância entre o alvo e o detector;

KE = energia cinética das partículas alfa;

θ = ângulo de dispersão.

A variação prevista, de partículas alfa detectadas, com ângulo é seguida de perto podados do contador de Geiger-Marsden, mostrados na Figura abaixo.

Cálculo do tamanho nuclear máximo

Espalhamento com diferentes parâmetros de impacto.

Para colisões frontais cabeças entre partículas alfa e o núcleo, toda a energia cinética ${\displaystyle \scriptstyle E=z{\frac {1}{2}}m.v_{o}^{2}}$ da partícula alfa é transformada em energia potencial e a partícula está em repouso.

A distância entre o centro da partícula alfa e o centro do núcleo (b) neste momento é um valor máximo para o raio, se é evidente a partir da experiência que as partículas não atingiram o núcleo.

Aplicando a energia potencial de Coulomb entre as cargas nos electrões e no núcleo, pode-se escrever:

${\displaystyle {\frac {1}{2}}.m.v^{2}={\frac {1}{4\pi \varepsilon _{o}}}.{\frac {q_{1}q_{2}}{b}}}$ / G ψ = E ψ = IGFF   E [tG+].... ..  

Reorganizando,

${\displaystyle {\frac {1}{4\pi \varepsilon _{o}}}{\frac {2.q_{1}q_{2}}{m.v^{2}}}}$ (1,6) / G ψ = E ψ = IGFF   E [tG+].... ..  

Para uma partícula alfa:

• ${\displaystyle m\;({\text{massa}})=6,7\times 10^{-27}\;kg}$
• ${\displaystyle q_{1}=2\times (1,6\times 10^{-19})C}$
• ${\displaystyle q_{2}\;({\text{para ouro}})=79\times (1,6\times 10^{-19})C}$
• ${\displaystyle v_{\;}({\text{velocidade inicial}})=2\times 10^{7}m/s}$

Substituindo estes valores na eqn.1,6, dá o valor do parâmetro de impacto de cerca de ${\displaystyle \scriptstyle 2,7\times 10^{14}m}$ .

O verdadeiro raio é cerca de ${\displaystyle \scriptstyle 7\times 10^{-15}m}$.